|
Semesteraufgabe ME/KT II SS ´98 Inhalt: 1. Allgemeines und Anmerkungen zur Aufgabe ME/KT
II 2.
Semesteraufgabe ME/KT II, SS ‘98 3 Leitfaden zur Auslegung und der Bezug zur
Vorlesung
|
|
1. Allgemeines und Anmerkungen zur Aufgabe ME/KT II Zur Bearbeitung der Semesteraufgabe ME/KT II ist es unumgänmglich sowohl Grundlagenliteratur und Vorlesungsskripte zu Maschinenelemente/Konstruktionstechnik und Mechanik als auch die DIN-, ISO- bzw. DIN/ISO-Normen und VDI-Richtlinien heranzuziehen. Dieses "Handout" enthält dagegen in erster Linie die Aufgabenstellung und ist darüber hinaus als Wegweiser und Anleitung zur Bearbeitung der ME/KT II Aufgabe gedacht. Dieser Text soll die Grundlage für weitere Dokumentationen zu ME/KT Lehre und Übungen sein, die in Kürze auch über die WWW-Seiten des IMK, Labor SHS, eingesehen werden können und weiter ausgebaut werden sollen. Fragen zur ME/KT II Aufgabe können auch über e-mail an die jeweiligen Betreuer oder an maeckel@hrz.uni-kassel.de gestellt werden. 1.1 Voraussetzungen und Motivation für die Teilnahme Es bestehen keine Voraussetzungen für den Einstieg bei der Semesterübung ME/KT II. Es wird jedoch der Besuch der Vorlesung ME/KT I bzw. II und die Mitarbeit an den Hörsaal- und Gruppenübungen sowie darüber hinaus die Vorlesung Mechanik I und die parallel dazu gehaltene Vorlesung Mechanik II empfohlen. Die Teilnahme an Vorlesungen und Übungen selbst ist (wie an Hochschulen i.d.R. üblich) freiwillig, denn letztendlich muß die entsprechende Klausur oder Übung bestanden werden. Der Anlaß für die Studentin oder den Studenten eine Vorlesung oder Übung zu besuchen, sollte es sein, einen Überblick über das Fach zu gewinnen und sich entsprechendes Fachwissen anzueignen. Es soll jedoch auch vorkommen, daß kein Interesse am Fach besteht und dieses auch nicht durch die Veranstaltung selbst geweckt werden kann. In diesen Fällen kommt als Motivation zur Teilnahme an der Übung leider nur noch (neben dem Unterhaltungswert) der entsprechende Wert und Inhalt für die Vorbereitung zur Klausur in Frage. Aber auch dem interessierten Einsteiger ist häufig der Ablauf der Übung sowie ihr Bezug zu Vorlesung bzw. zur Klausur aufgrund der fehlenden Hintergrundkenntnisse nicht direkt ersichtlich, wie aus den Erfahrungen und Rückmeldungen der vergangenen Übungen festgestellt wurde. Daher sollen in den folgenden Abschnitten ein allgemeiner Überblick zur Semesterübung des SS ‘97 gegeben werden, der nicht nur Anhaltspunkte für die Vorgehensweise bei der Bearbeitung und Lösung der Aufgaben geben, sondern der auch die Hintergründe hinsichtlich des Bezugs zur Vorlesung darstellen soll. Als zusätzlicher Motivationsschub werden auch Hinweise zum Bezug der Übung mit der Klausur gegeben. 1.2 Ablauf der Übung ME/KT II In der Vorlesung ME/KT I des ersten Semesters werden Grundlagen und Normen zum technischen Zeichnen, Toleranzangaben und Passungen (Skript I, Abschn. 1.1-1.4) etc. behandelt; in den Übungen wird das technische Zeichnen durch die Erstellung von Einzelteil- bzw. Fertigungszeichungen sowie einer einfachen Zusammenbauzeichnung nach vorgegebenen Maßen, Körpern und Bauteilen praktisch angewandt. Die Themen der Vorlesung können dem Vorlesungsskript entnommen werden. Einen Überblick gibt das Vorlesungsverzeichnis. Aufbauend auf diesen Grundkenntnissen sollen in der Übung ME/KT II erste Erfahrungen im freien Konstruieren nach einem vorgegebenen mechanischen Prinzip gesammelt werden. Hierzu wird im Gegensatz zu ME/KT I nur eine, dafür jedoch umfangreichere Aufgabe ausgegeben. Die Aufgabe soll, begleitet von den Hörsaal- und Gruppenübungen, während des Semesters bearbeitet werden. Das Ergebnis muß in Form einer technischen Zusammenbauzeichnung zusammen mit einer der Aufgabe entsprechende Bauteilauslegungen abgegeben werden. Die Zusammenbauzeichnung muß alle notwendigen Ansichten zur eindeutigen Beurteilung und zum Verständnis der Funktion und Konstruktion enthalten. Sie kann von Hand (Tusche auf Transparent) oder durch ein CAD-System erstellt werden. An dieser Stelle soll darauf hingewiesen werden, daß z.Z. keine Unterstützung hinsichtlich des CAD-Systems erfolgen kann. Im allgemeinen wird aus Zeitgründen die Handzeichnung (zuerst mit Bleistift auf Karton) bevorzugt. Durch die Bearbeitung einer umfangreicheren Aufgabe mit einem festen Abgabetermin am Ende der Vorlesungszeit (Termine beachten!), sollen auch die realen Arbeitsbedingungen hinsichtlich der Terminbindung geübt werden. Das Überschreiten dieser Abgabetermine fließt dazu in der Form einer Art "Konventionalstrafe" ein, die darin besteht, daß die Aufgabe durch Negativpunkte entsprechend der verspäteten Tage abgewertet wird. Es ist daher empfehlenswert mit dem in der Hörsaal- und Gruppenübung vorgegebenen Arbeitsschritten mitzuhalten. In den Hörsaalübungen wird die allgemeine theoretische Herangehensweise an die gestellte Aufgabe, hinsichtlich der Auslegungs- und Berechnungschritte, aufgezeigt. In den Gruppenübungen sollen diese konkret auf die ME/KT II Aufgabe selbständig bzw. in Gruppenarbeit angewandt werden. 1.3 Auswahl, Bearbeitung und Bewertung der Aufgabe Das Thema der Konstruktionsaufgabe ist in erster Linie so ausgewählt und gestaltet, daß die Thematik der Vorlesungen ME/KT I und II zur Anwendung und Berechnung von Maschinenelemente möglichst vielseitig abgedeckt wird (vgl. 1.1). Durch diese Vorgabe sind jedoch die Auswahlmöglichkeiten von der Thematik sowie der praktischem Anwendungsbezug eingeschränkt. Die Aufgabe darf z.B. noch keine Zahnräder oder Gleitlagerungen enthalten, die Inhalt von ME/KT III sind. Zur Bearbeitung der Aufgabe bewährt es sich, wenn in Gruppenarbeit die Zeichnungen gegenseitig hinsichtlich der Funktion, des Zusammenbaus, und der Anwendung und Einbau von Wälzlagern überprüft und nach Fehler in der Darstellung, nach Doppelpassungen etc. gesucht wird. Auch als Vorbereitung für die Klausur ist dies empfehlenswert, da auch dieses angewandte konstruktive Hintergrundwissen und Fähigkeiten zum allgemeinen Umgang mit Maschinenelementen einen Teil der ME/KT II Klausur darstellt. Als Beispiel sei hier die Anwendung und der Einbau von Wälzlagern erwähnt, von denen in der aktuellen Übung ein großer Teil der verschiedene Lagertypen verwendet werden soll. Der Schwerpunkt in der Bewertung der abgegeben Übungsleistung liegt vor allem auf der Funktionalität, aber auch auf den sachgemäßen Berechnungen, die zum Nachweis der Funktionalität unumgänglich sind. Die folgende Liste enthält die in ME/KT gebräuchlichen Bewertungskriterien und Korrekturkürzel, die einer entsprechenden Gewichtung in der Bewertung der Aufgabe unterliegen. Bewertungskriterien und Korrekturkürzel: Schwerwiegende Konstruktionsfehler Zisch = zwei Teile mit unterschiedlichen
Geschwindigkeiten berühren sich Darstellungs- und Gestaltungfehler GF = ungünstige Gestaltung hinsichtlich des
möglichen Fertigungsverfahrens
|
|
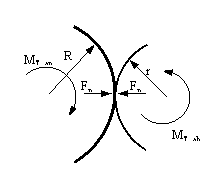
2. Semesteraufgabe ME/KT II, SS ‘98: Die Aufgabe des SS ’98 ist die Konstruktion eines stufenlosen Reibrad-Verstellgetriebes für Einzelfertigung. Hierzu sind die Anforderungen an den Entwurf in Form von technischen Daten und das Lösungsprinzip durch eine Funktionsskizze in den folgenden Abschnitten vorgegeben. 2.1 Hintergund und Prinzip stufenloser Wälzgetriebe Bei Verstellgetrieben ist im Gegensatz zu Schaltgetrieben das Übersetzungsverhältnis stufenlos regelbar. Je nach Bauart (Riemen- oder Reibradgetriebe) werden Wirkungsgrade von 0 bis über 0.9 erreicht. Reibradgetriebe übersetzen im allgemeinen gleichförmig durch Reibschluß zwischen glatten Laufflächen einer Reibradpaarung. Das Antriebsmoment MT, an bzw. die Umfangskraft Ft= MT/R der Reibradpaarung werden durch die Wälzreibung m entsprechend der Andruckkraft Fn übertragen (Bild 1).
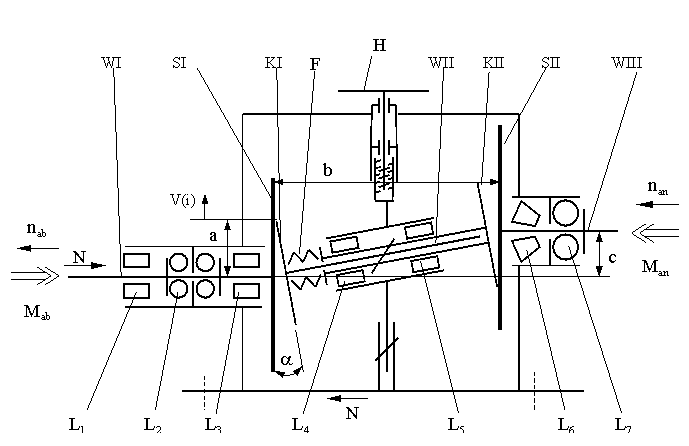
Bild 1 Reibradpaarung Reibradgetriebe weisen i.a. hohe Leistungsgewichte auf und eignen sich daher im Vergleich mit Zahnradgetrieben nur für begrenzte Leistungen. Grund hierfür ist, daß reibschlüssige Getriebe nur den Anteil m Fn als Umfangskraft übertragen. Bei Zahnradgetrieben (ME/KT III) hingegen kann infolge des Formschlusses die volle, nur durch die Hertzsche Pressung beschränkte Normalkraft übertragen werden. Reibradgetriebe sind jedoch entsprechend kostengünstiger und bei weichen Reibbelägen entsprechend geräuschärmer. Es lassen sich ferner hohe Übersetzungen ins Schnelle realisieren. Zusätzlich kann auch die Funktion des Ein- und Auskuppelns durch das Abheben der Reibräder sowie ein drehmomentabhängiger Überlastschutz durch Durchrutschen der Reibräder genutzt werden. 2.2 Klärung der Aufgabe und der Funktionen Aus der Funktionsskizze (Bild 2) ist zu entnehmen, daß die stufenlose Einstellung des Übersetzungsverhältnisses auf der Basis eines Reibradgetriebes mit Kegelrädern KI und KII gelöst werden soll. Die kegeligen Laufflächen bestehen aus angefasten Scheiben, die mittels Welle-Nabe-Verbindung auf der Welle II sitzen. Die Kegelmäntel drücken sich durch die Kraft der Feder F an Scheiben SI und SII an. Geometrisch besteht somit jeweils ein Linienkontakt zwischen den Scheiben und dem Kegelmantel. Entsprechend der Wälzreibung m kann so ein gewisses Drehmoment von der Antriebsseite des Getriebes an der Welle I über die Welle II auf die Welle III übertragen werden. Durch vertikales Verschieben der Welle II ändern sich der Abstand der Auflagepunkte der Kegelmäntel auf den Reibscheiben, so daß entsprechend der Verhältnisse der Abrollradien die Abtriebsdrehzahlen relativ zu den Antriebsdrehzahlen eingestellt werden können. Entsprechend der Drehzahl ändert sich auch das Abtriebsmoment, was speziell für die Festigkeitsauslegung zu berücksichtigen ist.
Bild 2: Funktionsskizze
zur aktuellen ME/KT II Aufgabe 2.3. Technische Vorgaben
2.4 Dokumentation Die Berechnungen sind nachvollziehbar darzustellen und nach den folgenden Punkten zu gliedern. Die entsprechend der Aufgabenpunkte geforderten Ergebnisse und die verwendeten Randbedingungen sind deutlich herauszuheben oder zu markieren (vgl. Formelle Richtlinien zur Ausarbeitung im Skript). Eine gut lesbare handschriftliche Form ist ausreichend.
|
|
3 Leitfaden zur Auslegung und der Bezug zur Vorlesung Die Aufgabenstellung enthält den Hinweis, daß die Konstruktion für ein Einzelanfertigung auszuführen ist. Entsprechend sind also Gestaltung in Hinblick auf die Fertigung und Werkstoffwahl (vgl. Skript I, Abschn. 1.5) vorzunehmen. Konkret bedeutet dies, daß
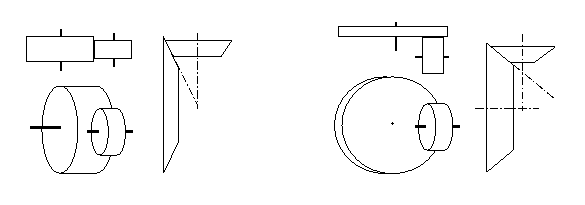
Die letzte Forderung begründet sich damit, daß der Konstrukteur bei einer Einzelfertigung ähnlich wie im Anlagenbau quasi nur einen "Versuch" hat und daher auf "Experimente" verzichtet werden. Es besteht nicht die Erwartung an die Konstruktion, unbedingt ein Optimum hinsichtlich bestimmter Kriterien zu erfüllen, welches meist erst in einer gewissen Entwicklungsreihe gefunden wird. Nachdem das Funktionsprinzip erkannt ist, sollte für die Auslegung entsprechend der Gliederung der Dokumentation vorgegangen werden, die mit der Vorauslegung zur Abschätzung der anzunehmenden Größe und Belastungen beginnt. 3.1 Vorauslegung (Punkt 1) Zur Vorauslegung gehört im wesentlichen eine grobe Abschätzung der Geometrie, die sich aus der Funktion und den Anforderungen ableiten läßt. Hier sind dies z.B. die zu übertragende Leistung bei vorgegebenen Drehzahlen und der Übersetzungsbereich etc.. Die vertikale Verschiebung der Welle II z.B. muß sich zwangsweise als eine Funktion der vorgegebenen Übersetzungsanforderung ergeben. Die geforderte Gesamtübersetzung iges ergibt sich aus dem Produkt der Einzelübersetzungen von Welle I zur Welle II und von Welle II zur Welle III. Die jeweilige Einzelübersetzung setzt sich wiederum aus den Winkelgeschwindigkeiten i=w a/w b bzw. den Drehzahlverhältnissen zusammen: iges = i1-2 i3-4 = (n1/n2) (n2/n4) = n1/n4. Da die Kegelräder auf einer Achse sitzen, sind die Drehzahlen trivialer Weise für beide gleich. Sind die Kegelräder K1 und K2 gleich groß liegt nur ein einstufiges Getriebe vor. Werden die Kegelräder jedoch nicht gleich groß gewählt, liegt ein zweistufiges Getriebe vor. Da nun die Geschwindigkeiten v = w r der Kegelflanke bei gleicher Winkelgeschwindigkeit aber bei unterschiedlichen Radien verschieden sind, ergibt sich die Gesamtübersetzung mit i=rb/ra entsprechend zu: iges = i1-2 i3-4 = (r2/r1) (r4/r3), In Worten ausgedrückt entspricht die Gesamtübersetzung dem Produkt aus den Radien der getriebenen zu den Radien der treibenden Rädern. Die Radien ändern sich entsprechend der vertikalen Verschiebung V nur an den Scheiben SI und SII. Nimmt man den Abstand a als Radius für die Übersetzung i=1:1 so wird r1=a+V und r4=a-V. Eingesetz in die Gleichung für die Gesamtübersetzung kann nach V aufgelöst werden. Im einfachen Fall für r2 ¹ r3 ergibt sich V(i) = a (i r2- r3)/(i r2+ r3) Es besteht jedoch laut Aufgabe die Bedingung, daß für die Übersetzung von 1:1 einwandfreie kinematische Abrollverhältnisse vorliegen müssen. Bei nicht einwandfreien kinematischen Abrollverhältnissen treten zusätzliche Wirkungsgradverluste und Verschleiß durch Bohrreibung und Bohrschlupf auf. Bei einander schneidenden Drehachsen ist nur dann ein einwandfreies kinematisches Abrollen der Berührflächen möglich, wenn ihre Wälzkegel auf zusammenfallenden Kegelspitzen liegen. Diese Verhältnisse liegen übertragen auf die Paarung Kegelrad–Scheibe nur genau dann vor, wenn sich die Spitze des Wälzkegels auf den Mittelpunkt der Scheibe (also den Schnittpunkt der Reibscheibenoberfläche mit seiner Wellenachse) trifft (Bild 4). Dies ist wiederum für den Fall der Übersetzung 1:1 nur dann möglich, wenn auch die Kegelscheiben gleich groß sind. Für r2 ¹ r3 erhält man: V(i) = a (1-i)/(1+i). Der Winkel a soll klein sein, um den überwiegenden Anteil der Federkräfte als Normalkraft in die Scheiben einzuleiten. Dabei kann akzeptiert werden, daß ein zusätzliches Kippmoment auf die Lager L4 und L5 ausgeübt wird. Resultierend aus den Größen a und a kann der Durchmesser der Welle II bzw. des mittleren Kegelraddurchmessers bestimmt werden.
Bild 3 Beispiele für kinematisch einwandfreie Abrollverhältnisse (links), nicht eindeutig (rechts) Die Antriebs- bzw. minimalen und maximalen Abtriebsdrehmomente lassen sich nach P=MTw aus der vorgegebenen Leistung und den entsprechenden Drehzahlen bei gegebenen Übersetzungsverhältnissen i unter der Annahme eines idealen Wirkungsgrades des Getriebes berechnen. Aus den an den Scheiben zu übertragenen Momenten können die erforderlichen Reibkräfte entsprechend der Abrollradien a +/- der Verschiebung V(i) nach der aus der Mechanik bekannten Beziehung M=F´ r abgeleitet werden. Mit dem gegebenen Haftreibwert m und dem Nutzgrad h läßt sich die minimal erforderliche Andruckkraft Fn nach der aus der Mechanik bekannten Beziehung Fr=m h Fn berechnen. Der tangentiale Nutzgrad h berücksichtigt, daß nur bei einem Übersetzungsverhältnis von i=1:1 im Falle dieses Kegelreibradgetriebes einwandfreie kinematische Abrollverhältnisse vorliegen. Diese Abschätzung der benötigten Mindestandruckkraft ist eine Grundlage für alle weiteren Auslegungsschritte der Punkte 2-7. In der Vorlesung ME/KT I werden die Grundlagen der Gestaltung von Maschinenelementen und Systemen (Skript I, Absch. 1.5) sowie die Grundlagen zur Festigkeitsberechnung (Skript I, Abschn. 1.6) behandelt. Die entsprechenden Berechnungsgrundlagen sind praktisch auf die jeweiligen Punkte hier in der Vorauslegung und auf die Punkte 2, 3 und 5 anzuwenden. In der Vorauslegung sollen im Gegensatz zu dem unter Punkt 5 durchgeführten Dauerfestigkeitsnachweis, jedoch nur überschlägig, ein erforderlicher Mindestdurchmesser für die Wellen I und II abgeschätzt werden, um eine Vorauswahl für den Durchmesser der Wälzlager treffen und damit eine erste Skizze der Wellen anfertigen zu können. 3.2 Festigkeitsnachweis der Reibscheiben (Punkt 2) Die Durchbiegung oder Festigkeit der Reibscheiben an der Nabe sollen in dieser Übung unberücksichtigt bleiben. Dafür soll der Wälzkontakt zwischen Kegel- und Reibscheibe untersucht werden. Im Wälzkontakt entsteht real unter Last infolge der Applattung der sich punkt- oder linienförmig berührenden Körper eine Berührfläche. Die maximalen Schubspannungen treten etwas unterhalb diese Druckfläche auf. Da die Schubspannungen proportional zur Hertzschen Pressung auftreten, soll der Festigkeitsnachweis der Reibscheiben bzw. Kegelräder vereinfacht auf der Grundlage der Hertzschen Pressung durchgeführt werden. Es soll jedoch bemerkt werden, daß diese vereinfachte Berechnung zur Hertzschen Pressung eigentlich nur für die alleinige Wirkung von Normalkräften, bei homogenem, isotropem Material und unter der Gültigkeit des Hookeschen Gesetzes anzuwenden ist. Zusätzlich zur Normalbelastung treten hier in der Berührzone auch trangentiale Reibkräfte auf, welche eine zunehmende und an die Oberfläche wandernde maximale Schubspannung bewirkt. Für die Hertzsche Pressung einer Linienberührung zweier Zylinder mit r1 und r2 gilt: pmax=s 0=-Ö [(F E)/(2p r l (1-n )] mit 1/r=1/r1+1/r2 Zur Berechnung der Hertzschen Pressung wird hier näherungsweise die Anpresspaarung von Ebene-Zylinder angenommen. Notwendig dazu ist die Errechnung eines äquivalenten Zylinderdurchmessers und die Grenzbetrachtung von r1® ¥ . In Abhängigkeit der Andruckkraft kann dann nach der Formel für die Hertzsche Pressung eine Mindestlänge für die Kantenlänge des sich ergebenden Kegelstumpfes für den statischen Fall unter ausschließlicher Berücksichtigung der Andruckkräfte festgelegt werden. Für die weiterführenden Rechnungen kann die resultierende Kraft in der Mitte der Auflagelinie bzw. Kegelkante angenommen werden. Hier soll bei der Festlegung der Kegelkantenlänge kein Sicherheitsfaktor berücksichtigt werden. Eine zu große Kegelkantenlänge zur Verminderung der Pressungen führt wiederum durch die nicht einwandfreien Abrollverhältnisse bei Übersetzungsverhältnissen ungleich 1 zu verstärkter Bohrreibung und somit zu einem erhöhten Wirkungsgradverlust des Getriebes. 3.3 Graphische Darstellung der angreifenden Kräfte und Momente an den Wellen (Punkt 3) In dieser Teilaufgabe wird die Vorgehensweise des Freischneidens aus der Mechanik angewendet. Die Schnittkräfte und Lagerreaktionen können einfach aus den Gleichungssystemen, resultierend aus dem Gleichgewicht der angreifenden Kräfte bzw. Momente, errechnet werden, da die Berechnung der angreifenden Kräfte und Momente hier nur für den stationären Betrieb des Getriebes erfolgen soll (Massenkräfte resultierend aus der Erdbeschleunigung und Bescheunigungen im Verstellbetrieb sollen vernachlässigt werden), so daß die Kenntnisse aus der Statik (Mechanik I+II) ausreichend sind. Hierzu wird empfohlen, das Problem in die einzelnen Ebenen des Koordinatensystems mit x als Wellenachse aufzuteilen. Die resultierenden Auflagerreaktionen zur Berechnung der Lagerlebensdauer unter Punkt 6 werden dann durch Vektoraddition wieder superponiert. Die qualitative Darstellung der Querkräfte und Momentenverläufe soll dazu verhelfen die für den Dauerfestigkeitsnachweis kritischen Stellen in Abhängigkeit der Schwachstellen wie z.B. durch Spannungskonzentrationen an Kerben zu identifizieren. Auch diese Transferleistung der Übertragung und Anwendung der Mechanik auf das reale Bauteil war bisher Teil der Klausur von ME/KT II. Hierzu mußte z.B. eine technische Zusammenbauzeichnung in ein mechanisches Ersatzsystem übertragen und entsprechend freigeschnitten werden sowie die Schnittkräfte über die Bauteilachse aufgetragen werden. 3.4 Dauerfestigkeitsberechnung (Punkt 5) Die Vorlesung ME/KT II vertieft die Festigkeitslehre (Skript II. Abschn. 2 und 3) und analysiert auf dieser Grundlage die stoff- und formschlüssigen Verbindungen des Maschinenbaus (Skript II, Abschn. 4 und 5). Auf dieser Basis soll zu Punkt 5 der Aufgabenstellung eine Dauerfestigkeitsberechnung durchgeführt werden. Aufgrund der zu berücksichtigenden Faktoren wie Kerbwirkung, Größenbeiwert, Oberflächenbeschaffenheit, Werkstoffwahl etc. ist der Dauerfestigkeitsnachweis erst nach einem Entwurf möglich. Hieran wird die meist notwendige iterative Vorgehensweise des Konstruktionsprozesses deutlich. Aus diesen Gründen wurde im Zuge der Vorauslegung eine überschlägige Berechnung der Wellendurchmesser durchgeführt. Endet der Dauerfestigkeitsnachweis dennoch nicht erfolgreich, kann jedoch in gewissen Grenzen durch entsprechende Kompensationsmaßnahmen ein Ausgleich erfolgen und die Rechnung wiederholt werden. Damit kann die Konstruktion "gerettet" werden, ohne eine komplette Änderung der Geometrie der Welle vornehmen zu müssen. Eine Möglichkeit besteht z.B. darin, einen anderen, aber dennoch sinnvollen Werkstoff mit höheren Dauerfestigkeitseigenschaften zu wählen. Eine andere Maßnahme könnte z.B. der Verminderung der Kerbwirkung dienen. Solche Beispiele und Maßnahmen werden in den Vorlesungen und Übungen erläutert. Auch die hier vermittelten Kenntnisse aus der Festigkeitsberechnung wurden (wiederum in Anlehnung an reale Maschinenbauteile oder in Form von prinzipiellen Fragen zum Verständnis) in den zurückliegenden ME/KT II Klausuren gefordert. 3.5 Berechnung der weiteren vorhandenen Maschinenelemente (Punkte 4, 6 und 7) Unter den Punkten 4, 6, und 7 der Aufgabenstellung wird hier die Auslegung einzelner Konstruktions- und Maschinenelemente, speziell entsprechend der Konstruktion z.B. Tellerfederelemente, Wälzlager und entsprechend der Aufgabe, Schraubenverbindungen oder Nabe-Welle-Verbindungen gefordert, die im Skript II in den Abschnitten 6-8 behandelt werden.
|
|
Die ME/KT II Semesteraufgabe dient also, wie aus dem obigen Abschnitt ersichtlich, nicht nur zur praktischen Anwendung des Vorlesungstoffes, sondern auch zur Vorbereitung für die Klausur. Für die überwiegende Mehrheit der TeilnehmerInnen müßte es sich also positiv auswirken, die Semesteraufgabe kontinuierlich und parallel zu den Übungen eigenständig durchzuführen.
|
|
Vortestat: Eine pausfähige Zusammenbauzeichung in Bleistift (ohne Teile-Nr., Dokumentation und Stückliste) ist in den Übungsgruppen (Termine nach Absprache mit dem Tutor) vorzulegen. Abgabe: Eine normgefaltete Zusammenbauzeichnung in Tusche, die Bleistiftzeichnung des Vortestats, Stückliste und Dokumentation unter Angaben von Name Matr.-Nr. und Tutor sind bis 17.7.1998, 12.00 Uhr abzugeben
|
bearbeitet von ganyimin@uni-kassel.de